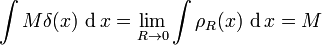Rotazioni angolari: vettoriali?

Facciamo prima un semplice esperimento e poi vediamo in dettaglio il suo significato fisico.

Prendiamo un libro, poniamolo sulla nostra scrivania (sdraiato sul piano orizzontale) e facciamolo ruotare di due angoli successivi:
-> prima di un angolo α=90° intorno all'asse verticale passante per il centro del libro (in senso orario visto dall'alto);
-> poi di un angolo β=90° intorno all'asse orizzontale passante per il centro del libro (in senso orario fissato un verso dell'asse).
Osserviamo quindi la posizione esatta del libro a cui ci ha condotto la rotazione consecutiva dei due angoli (cioè l'operazione α+β).
Nota: con α e β indichiamo sia gli angoli che le relative operazioni di rotazione, il cui uso è reso chiaro dal contesto.

Ora proviamo a fare le stesse operazioni di rotazione ma invertendo l'ordine, cioè prima applichiamo al libro la rotazione dell'angolo β e poi quella dell'angolo α. Con nostra sorpresa arriveremo ad una posizione finale diversa del nostro libro, da cui si può dedurre che in generale:

α+β≠β+α .

Nota: ciò in pratica significa che le operazioni di rotazione non obbediscono alla legge commutativa della somma.

La prima deduzione che possiamo trarre dal nostro esperimento è che le rotazioni angolari non possono essere considerate come se fossero dei vettori, poiché sappiamo che per essi vale la proprietà commutativa della somma.

Tuttavia ripetiamo l'esperimento per angoli diversi, più piccoli di 90°; ad esempio prima per 45° poi per 30° ed infine per soli 10°.

Se eseguiamo con precisione ogni rotazione e prendiamo nota della posizione iniziale e finale del libro, ci accorgiamo che man mano che gli angoli diventano sempre più piccoli, in pratica non si osservano differenze nel risultato finale (una volta invertito l'ordine delle rotazioni); perciò per piccoli angoli risulta:

α+β≈β+α

relazione sempre meno approssimata quanto minori sono gli angoli di rotazione.

In particolare deduciamo che se gli angoli sono infinitesimi (cioè se prendiamo dα e dβ) possiamo scrivere:

dα+dβ=dβ+dα

e quindi è corretto affermare che rotazioni angolari infinitesime possono essere rappresentate da vettori: basta infatti associare l'ampiezza elementare dell'angolo alla lunghezza del vettore e stabilire una direzione e un verso legato alla rotazione (ad esempio usando la regola della mano destra).

Questo non è un risultato di poco conto poiché ciò significa che altre grandezze fisiche, definite in termini di rotazioni angolari infinitesime, possono essere trattate a tutti gli effetti come dei vettori.

Prendiamo ad esempio la velocità angolare istantanea così definita:

w=dα/dt

che come è noto è rappresentata da un vettore; ma anche per l'accelerazione angolare si ha

a=dw/dt 

poiché la derivata di un vettore è a sua volta un vettore*.
Nota: invece la velocità angolare media w=∆α/∆t non può essere definita come un vettore poiché non dipende da una rotazione angolare infinitesima.

Ciò significa che in tutti questi casi, una volta associato il modulo della grandezza fisica alla lunghezza del vettore e stabiliti una direzione e un verso legato alla rotazione**, possiamo utilizzare tutto l'apparato formale dei vettori per trattare le grandezze vettoriali considerate.

(*) Se definiamo il vettore w(t)=iw_x(t)+jw_y(t)+kw_z(t) allora dw/dt=idw_x/dt+jdw_y/dt+kdw_z/dt=a è il vettore dell'accelerazione angolare; in particolare se w=cost. (ma dw/dt≠0) segue a_|_w: infatti se w²=ww=cost. allora dww/dt=wdw/dt+wdw/dt=0 e quindi wdw/dt=0).
(**) Ad esempio nel caso della velocità angolare istantanea il relativo vettore è definito lungo l'asse di rotazione e il verso determina il senso della rotazione, secondo la regola della mano destra (vedi Wikipedia).

La Delta di Dirac

Diamo subito la definizione della famosa delta di Dirac:
"Introdotta da Paul Dirac, anche se già presente nei lavori di Oliver Heaviside, è una funzione generalizzata che dipende da un parametro reale in modo tale che sia nulla per tutti i valori del parametro ad eccezione dello zero, ed il suo integrale sul parametro tra -∞ e +∞ sia pari a 1".
(Per tutti i dettagli vedi Wikipedia).

Ed ecco il grafico della delta di Dirac (come si vede non è propriamente una funzione, infatti nel punto x=0 non è ben definita ma tende a infinito)*:

 

Come si può intuire dal grafico, la delta di Dirac "viene utilizzata per rappresentare approssimativamente fenomeni come i picchi alti e stretti di alcune funzioni o le loro discontinuità: è lo stesso tipo di astrazione che si fa per la carica puntiforme, la massa puntiforme o l'elettrone puntiforme" (vedi Wikipedia).
Nota: in realtà la delta di Dirac non è propriamente una funzione ma una distribuzione che generalizza il concetto di funzione (vedi Wikipedia).
(Vedi anche l'ottima lezione di Marco Codegone sulle Distribuzioni)

Ma passiamo ora alla parte formale della definizione:
"Formalmente la delta di Dirac δ(x) viene definita dalla seguente notazione:

valida per ogni funzione continua ø(x) in un intorno dello zero" (vedi Wikipedia).
Nota: pur utilizzando il simbolo dell'integrale, l'operazione non è propriamente di integrazione, ma di applicazione del funzionale δ(x) alla funzione test ø(x).

In breve la funzione impropria δ(x) gode delle due seguenti proprietà:

δ(x)=0   per   x≠0

cioè δ(x) è sempre nulla tranne che in x=0 dove tende a infinito e inoltre:

cioè l'integrale di δ(x) è uguale a 1 se il punto x=0 è contenuto nell'intervallo di integrazione, altrimenti è nullo.

Nota: nell'integrale sopra compare per comodita la variabile t al posto di x ma nulla è cambiato.

Per mostrare il suo significato fisico vediamo una semplice applicazione; consideriamo cioè una massa puntiforme.
Come sappiamo nel caso generale di una massa M distribuita in un volume V possiamo scrivere, una volta definita la sua densità ρ(x)=M(x)/V (dove x indica un punto qulasiasi del corpo considerato):

e ciò significa che integrando la densità ρ(x) su tutto il volume V si ottiene la massa M. Tuttavia nel caso di una massa considerata puntiforme (come quella di un elettrone) non possiamo indicare la sua densità di massa come ρ(x)=M(x)/V perché per V-->0 avremmo un valore infinito (e un integrale nullo)** ma dobbiamo indicarla come Mδ(x) dove δ(x) è la delta di Dirac prima definita.

Infatti integrando Mδ(x) sul volume V avremo per la definizione della delta data sopra (poniamo ø(x)=1 e moltiplichiamo per M entrambi i membri dell'equazione che definisce la delta):

dove abbiamo indicato il passaggio al limite, di solito sottinteso, con il raggio R della particella che tende a zero (vedi Wikipedia).
Nota: in effetti si può mostrare che la delta può essere considerata proprio come il limite di alcune particolari successioni di funzioni, come ad esempio la funzione gaussiana (vedi Wikipedia).

(*) Si può immaginare una successione di funzioni che hanno picchi sempre più alti e diventano sempre più strette in x=0, mantenendo costante e pari a 1 l’area sotto la curva, con il valore della funzione che tende a zero in ogni punto, eccetto nello zero dove tende all’infinito.
(**) Si noti che l'integrale di densità di una massa puntiforme, essendo la densità infinita solo in un punto mentre è nulla nel resto dello spazio, è in realtà nullo secondo la misura di Lebesgue (vedi Wikipedia).